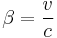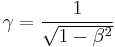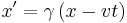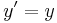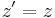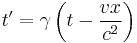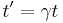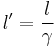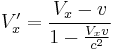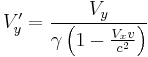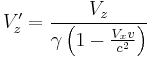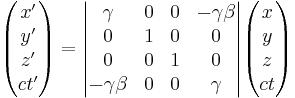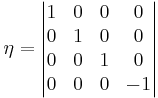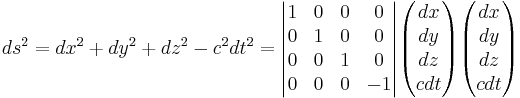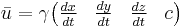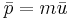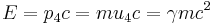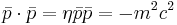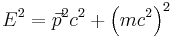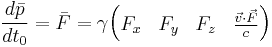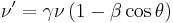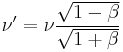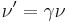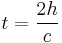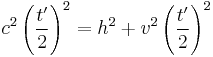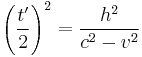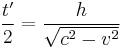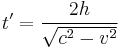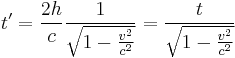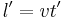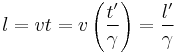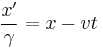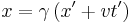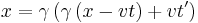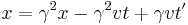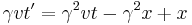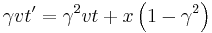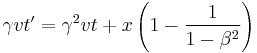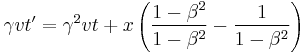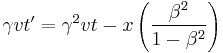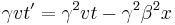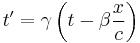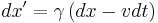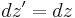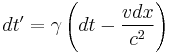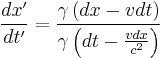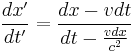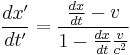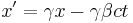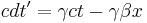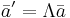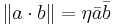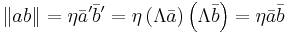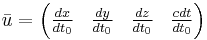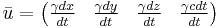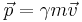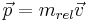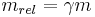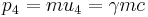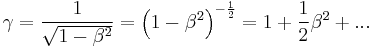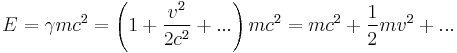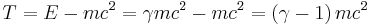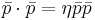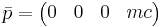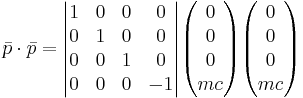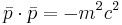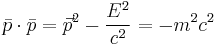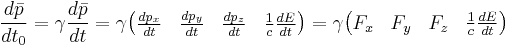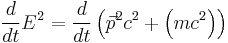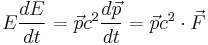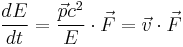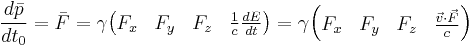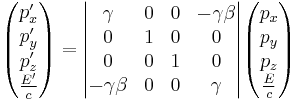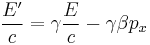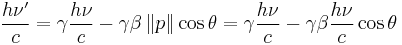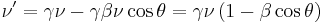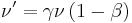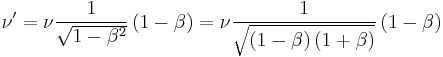List of relativistic equations
A list of relativistic equations:
Contents |
List of Equations
Lorentz Transformation
The Lorentz transformation:
Time dilation:
Length contraction:
Velocity Subtraction:
Four-Vectors and Matrices
The matrix version of the Lorentz transformation:
The metric tensor:
The space time interval:
Four velocity:
Four-momentum:
Energy in Relativity
Energy and the four-momentum's time term:
Kinetic energy:
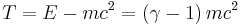
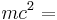 Rest Energy
Rest Energy
Other useful energy-momentum relations:
Four-force:
Doppler Shift
General Doppler shift:
Doppler shift for emitter and observer moving right towards each other (or directly away):
Doppler shift for emitter and observer moving in a direction perpendicular to the line connecting them:
Derivation of the equations of Special Relativity
To derive the equations of special relativity, one must start with two postulates:
- The laws of physics are invariant under transformations between inertial frames. Basically, the laws of physics will be the same whether you are testing them in a frame 'at rest', or a frame moving with a constant velocity relative to the 'rest' frame.
- The speed of light in a vacuum is measured to be the same by all observers in inertial frames. So, if I shine a beam of light, and measure how fast it's going, and then start moving really fast, and then measure the speed of the light beam again, both measurements will produce the same result.
From these two postulates, all of special relativity follows.
Time Dilation
Now, with the above postulates in mind, imagine you are in a train, a car, a bus, or any other vehicle, moving with a velocity  with respect to someone standing on the ground as your vehicle goes by. Inside your vehicle, you shine a light upwards to a mirror on the ceiling, where the light bounces back down. If the height of the mirror is
with respect to someone standing on the ground as your vehicle goes by. Inside your vehicle, you shine a light upwards to a mirror on the ceiling, where the light bounces back down. If the height of the mirror is  , and the speed of light
, and the speed of light  , then the time it takes for the light to go up and come back down is:
, then the time it takes for the light to go up and come back down is:
However, to the observer on the ground, the situation is very different. Because the train is moving by the observer on the ground, the light beam appears to move diagonally instead of straight up and down. To visualize this, picture the light being emitted at one point, then having the vehicle move until the light hits the mirror at the top of the vehicle, and then having the train move still more until the light beam returns to the bottom of the vehicle. The light beam will have appeared to have moved diagonally upward with the train, and then diagonally downward. This path will help form two-right sided triangles, with the height as one of the sides, and the two straight parts of the path being the respective hypotenuses:
Rearranging to get 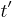 :
:
Taking out a factor of  , and then plugging in for
, and then plugging in for  , one finds:
, one finds:
This is the formula for time dilation. In particular, the following notations are used very often in special relativity:
This makes the formula for time dilation:
There are a few things worth pointing out here before moving on. First,  is one for two frames at rest, and gets progressively larger the closer to the speed of light the velocity between the two frames becomes. At the speed of light,
is one for two frames at rest, and gets progressively larger the closer to the speed of light the velocity between the two frames becomes. At the speed of light,  is effectively infinite. Second is that in this example the time measured in the frame on the vehicle,
is effectively infinite. Second is that in this example the time measured in the frame on the vehicle,  , is known as the proper time. The proper time between two events - such as the event of light being emitted on the vehicle and the event of light being received on the vehicle - is the time between the two events in a frame where the events occur at the same location. So, above, the emission and reception of the light both took place in the vehicle's frame, making the time that an observer in the vehicle's frame would measure the proper time.
, is known as the proper time. The proper time between two events - such as the event of light being emitted on the vehicle and the event of light being received on the vehicle - is the time between the two events in a frame where the events occur at the same location. So, above, the emission and reception of the light both took place in the vehicle's frame, making the time that an observer in the vehicle's frame would measure the proper time.
Length Contraction and the Lorentz Transformation
Consider a long train, moving with velocity  with respect to the ground, and one observer on the train and one on the ground, standing next to a post. The observer on the train sees the front of the train pass the post, and then, some time
with respect to the ground, and one observer on the train and one on the ground, standing next to a post. The observer on the train sees the front of the train pass the post, and then, some time 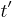 later, sees the end of the train pass the same post. He then calculates the train's length as follows:
later, sees the end of the train pass the same post. He then calculates the train's length as follows:
However, the observer on the ground, making the same measurement, comes to a different conclusion. This observer finds that time  passed between the front of the train passing the post, and the back of the train passing the post. Because the two events - the passing of each end of the train by the post - occurred in the same place in the ground observer's frame, the time this observer measured is the proper time. So:
passed between the front of the train passing the post, and the back of the train passing the post. Because the two events - the passing of each end of the train by the post - occurred in the same place in the ground observer's frame, the time this observer measured is the proper time. So:
This is the formula for length contraction. As there existed a proper time for time dilation, there exists a proper length for length contraction, which in this case is 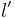 . The proper length of an object is the length of the object in the frame in which the object is at rest. Also, this contraction only affects the dimensions of the object which are parallel to the relative velocity between the object and observer. Thus, dimensions perpendicular to the direction of motion are unaffected by length contraction.
. The proper length of an object is the length of the object in the frame in which the object is at rest. Also, this contraction only affects the dimensions of the object which are parallel to the relative velocity between the object and observer. Thus, dimensions perpendicular to the direction of motion are unaffected by length contraction.
If you now plug in this result into the Galilean transformation, substituting  's for
's for 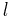 's, and assuming the velocity is wholly in the
's, and assuming the velocity is wholly in the  -direction, you get:
-direction, you get:
Or:
And going from the primed frame to the unprimed frame:
Going from the primed frame to the unprimed frame was accomplished by making  in the first equation negative, and then exchanging primed variables for unprimed ones, and vice versa. Also, as length contraction does not affect the perpendicular dimensions of an object, the following remain the same as in the Galilean transformation:
in the first equation negative, and then exchanging primed variables for unprimed ones, and vice versa. Also, as length contraction does not affect the perpendicular dimensions of an object, the following remain the same as in the Galilean transformation:
Finally, to figure out how  and
and 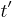 transform, you have to plug the
transform, you have to plug the  -to-
-to-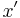 transformation into its reverse:
transformation into its reverse:
Plugging in the value for  :
:
Finally, dividing through by 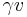 :
:
Or more commonly:
And the converse can again be gotten by changing the sign of  , and exchanging the unprimed variables for their primed counter-parts, and vice-versa. These transformations together are the Lorentz transformation:
, and exchanging the unprimed variables for their primed counter-parts, and vice-versa. These transformations together are the Lorentz transformation:
Velocity in Relativity
The Lorentz transformations also apply to differentials, so:
Now velocity is 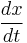 , so
, so
Now, putting in 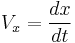 and
and 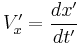 , you get the velocity addition - actually, the formulae below are subtraction, but addition is just flipping the various signs around - formula of special relativity:
, you get the velocity addition - actually, the formulae below are subtraction, but addition is just flipping the various signs around - formula of special relativity:
Also, the velocities in the directions perpendicular to the frame changes are affected, as shown above. This is due to time dilation, as encapsulated in the 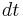 /
/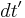 transformation. The
transformation. The 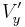 and
and 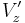 equations were both arrived at by dividing the appropriate space differential (e.g.
equations were both arrived at by dividing the appropriate space differential (e.g. 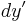 or
or 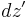 ) by the time differential.
) by the time differential.
The Metric and Four-Vectors
It is possible to express the above coordinate transformation via a matrix. To simplify things, it can be best to replace  ,
, 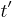 ,
, 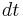 , and
, and 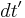 with
with 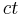 ,
, 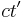 ,
, 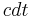 , and
, and 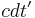 , which gives time the dimensions of a distance. So:
, which gives time the dimensions of a distance. So:
And, finally, in matrix form:
The vectors in the above transformation equation are known as four-vectors, in this case they are specifically the position four-vectors. In general, in special relativity, four-vectors can be transformed from one reference frame to another as follows:
In the above, 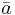 and
and 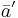 are the four-vector and the transformed four-vector, respectively, and
are the four-vector and the transformed four-vector, respectively, and 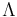 is the transformation matrix, which, for a given transformation is the same for all four-vectors one might want to transform. So
is the transformation matrix, which, for a given transformation is the same for all four-vectors one might want to transform. So 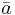 can be a four-vector representing position, velocity, or momentum, and the same
can be a four-vector representing position, velocity, or momentum, and the same 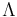 can be used when transforming between the same two frames.
can be used when transforming between the same two frames.
As with four vectors, there is a concept of the dot product, or the inner product. The form of this is:
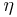 is known as the metric tensor. In special relativity, the metric tensor is as follows:
is known as the metric tensor. In special relativity, the metric tensor is as follows:
In the above, 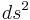 is known as the spacetime interval. Another thing worth noting is that this inner product is invariant under the Lorentz transformation. To have the inner product be invariant means the following:
is known as the spacetime interval. Another thing worth noting is that this inner product is invariant under the Lorentz transformation. To have the inner product be invariant means the following:
On a final note about the matrix and four-vector formulation of special relativity, the sign of the metric and the placement of the 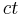 ,
, 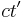 ,
, 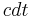 , and
, and 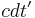 time-based terms can vary, with different people working in different standards. For instance, many times the time-based terms are placed first in the four-vectors, with the spatial terms following. Also, sometimes
time-based terms can vary, with different people working in different standards. For instance, many times the time-based terms are placed first in the four-vectors, with the spatial terms following. Also, sometimes 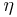 is replaced with
is replaced with 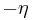 , making the spacial terms produce negative contributions to the dot product or spacetime interval, while the time term makes a positive contribution. These differences can be used in any combination, so long as the choice of standards is followed completely throughout the computations performed.
, making the spacial terms produce negative contributions to the dot product or spacetime interval, while the time term makes a positive contribution. These differences can be used in any combination, so long as the choice of standards is followed completely throughout the computations performed.
Velocity and Momentum
The relativistic four-velocity, that is the four-vector representing velocity in relativity, is defined as follows:
In the above, 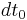 is the proper time of the path through spacetime, called the world-line, followed by the object velocity the above represents. As stated above in the derivation of time dilation, the proper time is the time between two events in a frame of reference where they take place at the same location. With the example of time dilation in mind, one can use the formula for it,
is the proper time of the path through spacetime, called the world-line, followed by the object velocity the above represents. As stated above in the derivation of time dilation, the proper time is the time between two events in a frame of reference where they take place at the same location. With the example of time dilation in mind, one can use the formula for it, 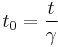 as follows:
as follows:
The first three terms, excepting the factor of  , is the velocity as seen by the observer in their own reference frame. The
, is the velocity as seen by the observer in their own reference frame. The  is determined by the velocity between the observer's reference frame and the object's frame, which is the frame in which its proper time is measured. This quantity is invariant under Lorentz transformation, so to check to see what an observer in a different reference frame sees, one simply multiplies the velocity four-vector by the Lorentz transformation matrix between the two reference frames.
is determined by the velocity between the observer's reference frame and the object's frame, which is the frame in which its proper time is measured. This quantity is invariant under Lorentz transformation, so to check to see what an observer in a different reference frame sees, one simply multiplies the velocity four-vector by the Lorentz transformation matrix between the two reference frames.
The four-momentum of an object is relatively straightforward:
This definition is identical in form to the relation to the classical momentum and the classical velocity. The mass,  is also its usual self. For the spatial portion of the four-momentum one gets:
is also its usual self. For the spatial portion of the four-momentum one gets:
In the above, the factor of  comes from the definition of the four-velocity described above. This formulation also has an alternative way of being stated:
comes from the definition of the four-velocity described above. This formulation also has an alternative way of being stated:
This formulation makes the new relation between the spatial velocity and the spatial momentum look practically identical. However, this can be misleading, as it is not appropriate in special relativity in all circumstances. For instance, kinetic energy and force in special relativity can not be written exactly like their classical analogues by only replacing the mass with the relativistic mass. Moreover, under Lorentz transformations, this relativistic mass is not invariant, while the regular mass is. That is why many people find it easier to just stick with the regular mass, and discard the relativistic mass.
Energy
There is one last feature of the four-momentum worth discussing, and that is the role of the time-based term, which will be called 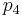 , as above the time term has been the fourth component of a four-vector. This term works out to be:
, as above the time term has been the fourth component of a four-vector. This term works out to be:
As it turn out, this is directly related to the energy in special relativity as follows:
This is the reason that the momentum four-vector is sometimes called the momentum-energy four-vector. However, it is not clear that this definition corresponds to the definition of the energy of a free particle classically, which is just the particle's kinetic energy. However, if you use the binomial series expansion of  for small velocities, you see the following:
for small velocities, you see the following:
The second term above is the classical kinetic energy. The first term is something new entirely, and reduces to Einstein's famous equation 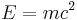 when the object is not moving. This term is called the rest mass. In addition to the classical term and the rest mass term, there are more terms that could be added to the expansion, but they all involve factors of at least
when the object is not moving. This term is called the rest mass. In addition to the classical term and the rest mass term, there are more terms that could be added to the expansion, but they all involve factors of at least 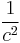 , which, for the approximation that the velocity is much less than the speed of light, mean that they are negligible and not easily detectable.
, which, for the approximation that the velocity is much less than the speed of light, mean that they are negligible and not easily detectable.
Taking the above expansion into account, noting that an object with zero velocity has energy equal to 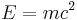 , one can show that the kinetic energy in special relativity is:
, one can show that the kinetic energy in special relativity is:
A few other useful energy and momentum relations
If one moves to the rest frame of an object, and then takes the dot-product of their four-momentums, one gets:
As the four-momentum is Lorentz invariant, the dot product of the four-momentum with itself is invariant under Lorentz transformations, so the above relation is true for the four-momentum in any frame of reference. In fact, assuming that there are spatial momentum terms, you can produce another relation:
In the above, 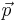 is the relativistic three velocity.
is the relativistic three velocity.
Force
A relativistic force, one that is invariant under the Lorentz transformation, can be formulated in a similar fashion to how the four-velocity was formulated. In the case of the four-velocity, this was arrived at by taking the derivative of four-position with respect to proper time, in an analogous fashion to the classical definition of valeocity as the derivative of position by time. Similarly, classical force was defined as the time derivative of momentum with time. So you can, in a similar fashion you can take the derivative of four-momentum with respect to proper time:
You can simplify the last term by noting that 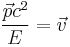 , you can do the following:
, you can do the following:
It should be noted that in the above, it is assumed that the mass is constant over time. Plugging this into the first result:
This is the relativistic four-force, which is invariant under Lorentz transformation.
Doppler Shift
If an object emits a beam of light or radiation, the frequency, wavelength, and energy of that light or radiation will look different to a moving observer than to one at rest with respect to the emitter. If one assumes that the observer is moving with respect to the emitter along the x-axis, then the standard Lorentz transformation of the four-momentum, which includes energy, becomes:
Now, if 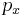 is
is 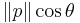 , where
, where  is the angle between
is the angle between 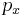 and
and 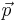 , and plugging in the formulas for frequency's relation to momentum and energy:
, and plugging in the formulas for frequency's relation to momentum and energy:
This is the formula for the relativistic doppler shift where the difference in velocity between the emitter and observer is not on the x-axis. There are two special cases of this equation. The first is the case where the velocity between the emitter and observer is along the x-axis. In that case 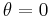 , and
, and 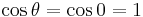 , which gives:
, which gives:
This is the equation for doppler shift in the case where the velocity between the emitter and observer is along the x-axis. The second special case is that where the relative velocity is perpendicular to the x-axis, and thus 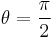 , and
, and 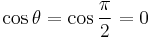 , which gives:
, which gives:
This is actually completely analogous to time dilation, as frequency is one over time. So, doppler shift for emitters and observers moving perpendicular to the line connecting them is completely due to the effects of time dilation.
See also
See also: